Function to get 5-sided polygon (pentagon) or star (pentagram) co-ords.
<?php
function _makeFiveSidedStar( $x, $y, $radius, $shape='polygon', $spiky=NULL ) {
$point = array() ; // new array
$angle = 360 / 5 ;
$point[0]['x'] = $x ;
$point[0]['y'] = $y - $radius ;
$point[2]['x'] = $x + ( $radius * cos( deg2rad( 90 - $angle ) ) ) ;
$point[2]['y'] = $y - ( $radius * sin( deg2rad( 90 - $angle ) ) ) ;
$point[4]['x'] = $x + ( $radius * sin( deg2rad( 180 - ( $angle*2 ) ) ) ) ;
$point[4]['y'] = $y + ( $radius * cos( deg2rad( 180 - ( $angle*2 ) ) ) ) ;
$point[6]['x'] = $x - ( $radius * sin( deg2rad( 180 - ( $angle*2 ) ) ) ) ;
$point[6]['y'] = $y + ( $radius * cos( deg2rad( 180 - ( $angle*2 ) ) ) ) ;
$point[8]['x'] = $x - ( $radius * cos( deg2rad( 90 - $angle ) ) ) ;
$point[8]['y'] = $y - ( $radius * sin( deg2rad( 90 - $angle ) ) ) ;
if( $shape == 'star' ) {
if( $spiky == NULL ) $spiky = 0.5 ; // degree of spikiness, default to 0.5
$indent = $radius * $spiky ;
$point[1]['x'] = $x + ( $indent * cos( deg2rad( 90 - $angle/2 ) ) ) ;
$point[1]['y'] = $y - ( $indent * sin( deg2rad( 90 - $angle/2 ) ) ) ;
$point[3]['x'] = $x + ( $indent * sin( deg2rad( 180 - $angle ) ) ) ;
$point[3]['y'] = $y - ( $indent * cos( deg2rad( 180 - $angle ) ) ) ;
$point[5]['x'] = $x ;
$point[5]['y'] = $y + ( $indent * sin( deg2rad( 180 - $angle ) ) ) ;
$point[7]['x'] = $x - ( $indent * sin( deg2rad( 180 - $angle ) ) ) ;
$point[7]['y'] = $y - ( $indent * cos( deg2rad( 180 - $angle ) ) ) ;
$point[9]['x'] = $x - ( $indent * cos( deg2rad( 90 - $angle/2 ) ) ) ;
$point[9]['y'] = $y - ( $indent * sin( deg2rad( 90 - $angle/2 ) ) ) ;
}
ksort( $point ) ;
$coords = array() ; // new array
foreach( $point as $pKey=>$pVal ) {
if( is_array( $pVal ) ) {
foreach( $pVal as $pSubKey=>$pSubVal ) {
if( !empty( $pSubVal ) ) array_push( $coords, $pSubVal ) ;
}
}
}
return $coords ;
}
$values = _makeFiveSidedStar( 100, 100, 50, 'star' ) ;
?>imagepolygon
(PHP 4, PHP 5, PHP 7, PHP 8)
imagepolygon — 绘制多边形
说明
自 PHP 8.0.0 起的签名(不支持命名参数)
替代签名(从 PHP 8.1.0 开始弃用)
imagepolygon() 在指定 image 中创建多边形。
参数
-
image 由图象创建函数(例如imagecreatetruecolor())返回的 GdImage 对象。
points-
包含多边形顶点的数组,例如:
points[0] = x0 points[1] = y0 points[2] = x1 points[3] = y1 num_points-
点(顶点)的总数,必须最少为 3。
如果根据第二个签名省略此参数,则points必须具有偶数个元素,并且假定num_points为count($points)/2。 color-
颜色标识符使用 imagecolorallocate() 创建。
示例
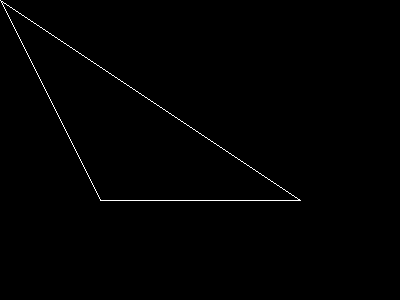
示例 #1 imagepolygon() 示例
<?php
// 创建空白图像
$image = imagecreatetruecolor(400, 300);
// 为多边形分配颜色
$col_poly = imagecolorallocate($image, 255, 255, 255);
// 绘制多边形
imagepolygon($image, array(
0, 0,
100, 200,
300, 200
),
$col_poly);
// 输出图像到浏览器
header('Content-type: image/png');
imagepng($image);
?>以上示例的输出类似于:
参见
- imagefilledpolygon() - 绘制多边形并填充
- imageopenpolygon() - Draws an open polygon
- imagecreate() - 创建新的基于调色板的图像
- imagecreatetruecolor() - 新建真彩色图像
+添加备注
用户贡献的备注 3 notes
tatlar at yahoo dot com ¶
19 years ago
licson0729 at gmail dot com ¶
13 years ago
Function to draw a n-sided regular polygon
<?php
$img = imagecreatetruecolor(1360,768);
function regularPolygon($img,$x,$y,$radius,$sides,$color)
{
$points = array();
for($a = 0;$a <= 360; $a += 360/$sides)
{
$points[] = $x + $radius * cos(deg2rad($a));
$points[] = $y + $radius * sin(deg2rad($a));
}
return imagepolygon($img,$points,$sides,$color);
}
regularPolygon($img,1360/2,768/2,300,8,0xffffff);//Test draw
header('Content-type: image/png');
imagepng($img);
imagedestroy($img);
?>
jsnell at networkninja dot com ¶
24 years ago
Here are some handy routines for rotation and translation of polygons. Scaling could be added easily as well.
<?php
function translate_point(&$x,&$y,$angle,$about_x,$about_y,$shift_x,$shift_y)
{
$x -= $about_x;
$y -= $about_y;
$angle = ($angle / 180) * M_PI;
/* math:
[x2,y2] = [x, * [[cos(a),-sin(a)],
y] [sin(a),cos(a)]]
==>
x = x * cos(a) + y*sin(a)
y = x*-sin(a) + y*cos(a)
*/
$new_x = $x * cos($angle) - $y * sin($angle);
$new_y = $x * sin($angle) + $y * cos($angle);
$x = $new_x+ $about_x + $shift_x ;
$y = $new_y + $about_y + $shift_y;
}
function translate_poly($point_array, $angle, $about_x, $about_y,$shift_x,$shift_y)
{
$translated_poly = Array();
while(count($point_array) > 1)
{
$temp_x = array_shift($point_array);
$temp_y = array_shift($point_array);
translate_point($temp_x, $temp_y, $angle, $about_x, $about_y,$shift_x, $shift_y);
array_push($translated_poly, $temp_x);
array_push($translated_poly, $temp_y);
}
return $translated_poly;
}
?>